Grey Wolf Optimization Algorithm In MATLAB

The Grey Wolf Optimization (GWO) algorithm is a nature-inspired optimization technique based on the social hierarchy and hunting mechanism of grey wolves. It is widely used in MATLAB for solving complex optimization problems.

Get Project Help Explore MATLAB Projects
Genetic Algorithm Illustration

About Grey Wolf Optimization Algorithm

Abstract

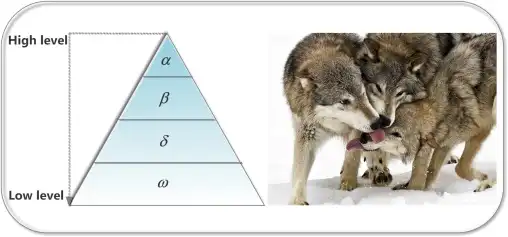
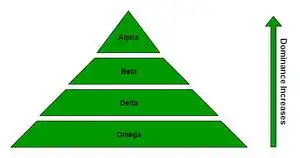
A new meta-heuristic called Grey Wolf Optimizer (GWO) inspired by grey wolves (Canis lupus). The GWO algorithm mimics the leadership hierarchy and hunting mechanism of grey wolves in nature. Four types of grey wolves such as alpha, beta, delta, and omega are employed for simulating the leadership hierarchy. In addition, the three main steps of hunting, searching for prey, encircling prey, and attacking prey, are implemented. The algorithm is then benchmarked on 29 well-known test functions, and the results are verified by a comparative study with Particle Swarm Optimization (PSO), Gravitational Search Algorithm (GSA), Differential Evolution (DE), Evolutionary Programming (EP), and Evolution Strategy (ES). The results show that the GWO algorithm is able to provide very competitive results compared to these well-known meta-heuristics. The paper also considers solving three classical engineering design problems (tension/compression spring, welded beam, and pressure vessel designs) and presents a real application of the proposed method in the field of optical engineering.

Introduction

Grey Wolf Optimization (GWO) algorithm simulates the leadership hierarchy and hunting strategies of grey wolves to solve optimization problems. MATLAB offers a robust platform for implementing GWO, enabling researchers to model and solve complex engineering and scientific challenges efficiently.

Related Work

Grey wolf optimizer (GWO) is a population-based meta-heuristics algorithm that simulates the leadership hierarchy and hunting mechanism of grey wolves in nature, and it’s proposed by Seyedali Mirjalili et al. in 2014.

Wolf Algorithms
  1. Alpha α wolf is considered the dominant wolf in the pack and his/her orders should be followed by the pack members.
  2. Beta β are subordinate wolves, which help the alpha in decision-making and are considered as the best candidate to be the alpha.
  3. Delta δ wolves have to submit to the alpha and beta, but they dominate the omega. There are different categories of delta-like Scouts, Sentinels, Elders, Hunters, Caretakers etc.
  4. Omega ω wolves are considered as the scapegoat in the pack, are the least important individuals in the pack and are only allowed to eat at last.
Wolf Algorithms

Main phases of grey wolf hunting:

  1. Tracking, chasing and approaching the prey.
  2. Pursuing, encircling, and harassing the prey until it stops moving.
  3. Attack towards the prey.

The social hierarchy and hunting behaviour of grey wolves are mathematically modeled to design GWO.

Why Use Grey Wolf Optimization Algorithm in MATLAB?

Efficient Optimization
AI & ML Integration
Complex Problem Solving
Robotics & Engineering

Applications of Grey Wolf Optimization Algorithm

Neural Network Training

Optimize neural network weights and architectures effectively.

Portfolio Optimization

Helps in financial modeling and optimal portfolio allocation.

Robotics Path Planning

Design efficient paths for autonomous robots using GA in MATLAB.

Need Help with Your MATLAB Genetic Algorithm Project?

Our experts provide end-to-end assistance for academic and professional MATLAB projects.

Hire an Expert Now