Is there a better way of solving simultaneous differential
Is there a better way of solving simultaneous differential equations then using dsolve as MATLAB crashes everytime I use it? So I have a set of simulataneous differential equtions that need to be solved as such: Ive been using this code but as stated in the title MATLAB crashes is there any better way of doing this: clear clc syms P1(t) P2(t) P3(t) P4(t) P5(t) P6(t) P7(t) P8(t)... Lam1 Lam2 Lam3 Mu1 Mu2 Mu3 % Typing in all the equations eqns = ... [diff(P1,t) == (-Lam1-Lam2-Lam3)*P1 + (Mu1)*P2 + (Mu2)*P3 + (Mu3)*P4,... diff(P2,t) == (Lam1)*P1 + (-Mu1-Lam2-Lam3)*P2 + (Mu2)*P5 + (Mu3)*P6,... diff(P3,t) == (Lam2)*P1 + (-Mu2-Lam1-Lam3)*P3 + (Mu1)*P5 + (Mu3)*P7,... diff(P4,t) == (Lam3)*P1 + (-Mu3-Lam1-Lam2)*P4 + (Mu1)*P6 + (Mu2)*P7,... diff(P5,t) == (Lam2)*P2 + (Lam1)*P3 + (-Mu1-Mu2-Lam3)*P5 + (Mu3)*P8,... diff(P6,t) == (Lam3)*P2 + (Lam1)*P4 + (-Mu1-Mu3-Lam2)*P6 + (Mu2)*P8,... diff(P7,t) == (Lam3)*P3 + (Lam2)*P4 + (-Mu2-Mu3-Lam1)*P7 + (Mu1)*P8,... diff(P8,t) == (Lam3)*P5 + (Lam2)*P6 + (Lam1)*P7 + (-Mu1-Mu2-Mu3)*P8] % Solutions Solver sol = dsolve(eqns, P1(0) == 1, P2(0) == 0, P3(0) == 0, P4(0) == 0,P5(0) == 0, P6(0) == 0,... P7(0) == 0, P8(0) == 0) % Printing the Solutions solP1(t)= sol.P1 solP2(t)= sol.P2 solP3(t)= sol.P3 solP4(t)= sol.P4 solP5(t)= sol.P5 solP6(t)= sol.P6 solP7(t)= sol.P7 solP8(t)= sol.P8
Prashant Kumar answered .
2025-11-20
You have a linear system:
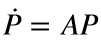
so the solution is going to be the matrix exponential:
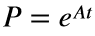
that in MATLAB code is:
syms P(t) Lam1 Lam2 Lam3 Mu1 Mu2 Mu3 t
A = [ - Lam1 - Lam2 - Lam3, Mu1, Mu2, Mu3, 0, 0, 0, 0
Lam1, - Lam2 - Lam3 - Mu1, 0, 0, Mu2, Mu3, 0, 0
Lam2, 0, - Lam1 - Lam3 - Mu2, 0, Mu1, 0, Mu3, 0
Lam3, 0, 0, - Lam1 - Lam2 - Mu3, 0, Mu1, Mu2, 0
0, Lam2, Lam1, 0, - Lam3 - Mu1 - Mu2, 0, 0, Mu3
0, Lam3, 0, Lam1, 0, - Lam2 - Mu1 - Mu3, 0, Mu2
0, 0, Lam3, Lam2, 0, 0, - Lam1 - Mu2 - Mu3, Mu1
0, 0, 0, 0, Lam3, Lam2, Lam1, - Mu1 - Mu2 - Mu3];
P = expm(A*t)
My Ryzen 7 1700 machine has been working on this for the past hour and does not appear to be close to finishing. I’m stopping it now, and will let you pursue this.