Problem with standard methods of smoothening in Signals

Illustration
Satya - 2024-02-12T22:22:21+00:00
Question: Problem with standard methods of smoothening in Signals

I'm encountering a challenge in MATLAB related to signal processing using the Signal Processing Toolbox. I have a noisy signal that I need to filter to extract meaningful information. The signal contains both high-frequency noise and low-frequency drift. My goal is to design a filter that effectively removes the noise while preserving the underlying signal characteristics. I've attempted to use standard filtering techniques, but I'm not satisfied with the results due to either over-smoothing or residual noise. Can someone provide guidance on how to design an optimal filter for this scenario, considering both the high-frequency noise and low-frequency drift present in the signal?

Related Questions

  • DTMF tone using matlab
  • How can I make the FREQZ function (in the Signal Processing or Filter
  • Using cellfun for multidimensional cell
  • How can I slice an audio from the front, and extract and save audio from the back.
  • Why do I receive two different responses when I try to discretize the same analog filter using the ELLIP

    • Expert Answer

    Profile picture of John Williams John Williams answered . 2025-11-20

    Hi Satya,
     
    I understand that you have a noisy signal containing both high-frequency noise and low-frequency drift, and you want to design an optimal filter to effectively remove the noise while preserving the underlying signal characteristics.
     
    Assumption: The noisy signal is sampled at a sufficient frequency to capture both high-frequency noise and low-frequency drift.
    To address this issue, you can utilize a combination of high-pass and low-pass filtering techniques to target the removal of both high-frequency noise and low-frequency drift while preserving the desired signal content.
     
    One approach is to use a cascaded filter design, where a high-pass filter is applied first to remove the low-frequency drift, followed by a low-pass filter to attenuate the high-frequency noise. Additionally, adaptive filtering techniques such as the Kalman filter can be effective in separating the signal from noise, especially when the characteristics of the noise are known or can be estimated.
     
    Below is an example demonstrating a cascaded filter design using a high-pass and low-pass filter:
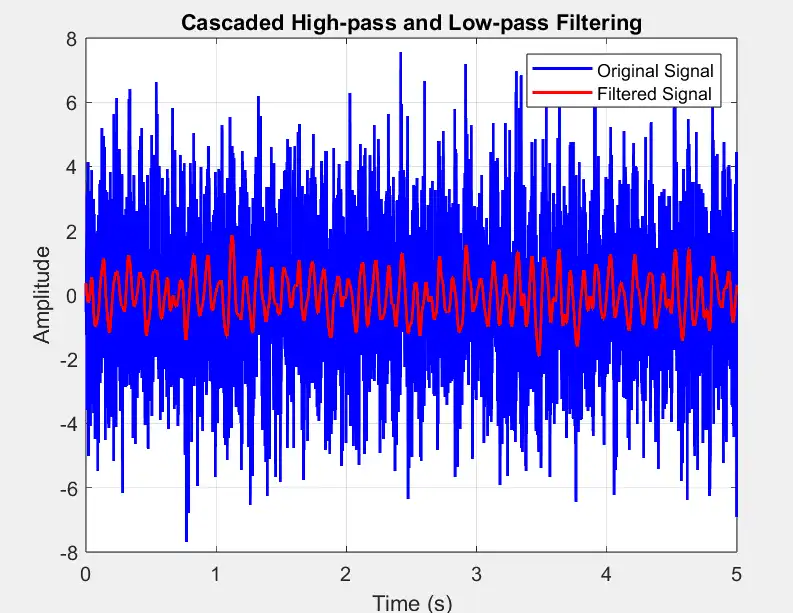
    % Generate noisy signal (example)
fs = 1000; % Sampling frequency
t = 0:1/fs:5; % Time vector
signal = sin(2*pi*10*t) + 0.5*sin(2*pi*50*t) + 2*randn(size(t)); % Noisy signal

% Design high-pass filter to remove low-frequency drift
highpass_cutoff = 0.5; % Cutoff frequency for high-pass filter (adjust as needed)
hp_filter = designfilt('highpassfir', 'FilterOrder', 50, 'CutoffFrequency', highpass_cutoff, 'SampleRate', fs);

% Design low-pass filter to attenuate high-frequency noise
lowpass_cutoff = 30; % Cutoff frequency for low-pass filter (adjust as needed)
lp_filter = designfilt('lowpassfir', 'FilterOrder', 50, 'CutoffFrequency', lowpass_cutoff, 'SampleRate', fs);

% Apply high-pass filter
filtered_signal = filtfilt(hp_filter, signal);

% Apply low-pass filter
filtered_signal = filtfilt(lp_filter, filtered_signal);

% Plot original and filtered signals
figure;
plot(t, signal, 'b', 'LineWidth', 1.5); hold on;
plot(t, filtered_signal, 'r', 'LineWidth', 1.5);
xlabel('Time (s)');
ylabel('Amplitude');
legend('Original Signal', 'Filtered Signal');
title('Cascaded High-pass and Low-pass Filtering');
grid on;
    Output observed:
    Please Note: The following output is generated for the sample data simulated. Please use your actual data and do adjustments to the filter parameters so that it fits to your use case.


    Not satisfied with the answer ?? ASK NOW

    Get a Free Consultation or a Sample Assignment Review!

    Upload Assignment Talk to Expert