why is my ea not being recognized?

Illustration
Clinton Mitchell - 2023-09-08T11:10:55+00:00
Question: why is my ea not being recognized?

clc; clear all; L = 1.25; E = 50000; I = 30000; w0 = 2.5; syms x f(x) = (w0/(120*E*I*L))*(-x^5+2*(L^2)*(x^3)-(L^4)*x); df = diff(f,x); true = df(2); roots = solve(f==0, x); true_roots = double(roots); xl = 200; xu = 300; xr = (xl + xu) / 2; es = 0.001; xr_new(1) = xr; if f(xl) * f(xu) < 0 disp('The function changes sign within this bound') for i = 1:100 val(i) = f(xl) * f(xr_new(i)); if val(i) < 0 disp('The root lies in the lower interval') xu = xr_new(i); elseif val(i) > 0 disp('The root lies in the upper interval') xl = xr_new(i); else val = 0; fprintf('The approximate root of the function is %1.2f \n',xr_new(i)) break end xr_new(i+1) = (xl + xu) / 2; ea = abs((xr_new(i+1) - xr_new(i))./xr_new(i+1)); if ea < es break end end else disp('The function does not change sign within this bound') end The function does not change sign within this bound % Print the results ea = ea*100; Unrecognized function or variable 'ea'. fprintf('The absolute approximate error is: %1.5f \n',ea) n_iterations = i+1; fprintf('The total number of iterations are: %d \n',n_iterations) root = xr_new(1,end); fprintf('The approximate root of the function is: %1.5f \n', root) x1 = -1000 : 1000; y1 = f(x1); y = double(y1); xmin = -1000; xmax = 1000; ymin = -0.5; ymax = 0.5; plot(x1, y1) hold on plot(true_root,0,'mo','MarkerFaceColor','m') set(gca,'XAxisLocation','origin','YAxisLocation','origin','XMinorTick','on') xlabel('x \rightarrow') ylabel('\uparrow f(x)') title('Graphical root')  

Related Questions

  • How do I uninstall and reinstall MathWorks Service Host?
  • MatLab App Design - how to use default value for Edit Field function?
  • What's the difference between imagesc and imshow?
  • Error evaluating parameter 'Value' in simulink
  • Why do I get a connection error when installing or activating MATLAB or other MathWorks products?

    • Expert Answer

    Profile picture of Prashant Kumar Prashant Kumar answered . 2025-11-20

    There are a few inconsistencies.
     
    (1) The simulation in [for ... end] loop never reached due to if condition f(xl)*f(xu) <0. The actual values of f(xl)*f(xu) were in sym and greater than 0. Therefore, by changing it to double and the if condition (f(xl)*f(xu)>), you will get the simulation results.
     
    (2) The found true roots were in sym.
     
    (3) Similarly, y1 = f(x1) was in sym that need to be numerical. Thus, double() is needed.
     
    (4) if val = 0 is not correct that must be val == 0.
     
    (5) It is better (must be) to use fplot() instead of plot to plot actual faction. By this way tru solutions can be shown explicitly - see figure (2).
     
    Here is the corrected code:
     
     
    clc; clearvars;
L = 1.25; E = 50000; I = 30000; w0 = 2.5;
syms f(x)
f(x) = (w0/(120*E*I*L))*(-x^5+2*(L^2)*(x^3)-(L^4)*x);
df = diff(f,x); 
true = double(df(2)); 
roots = vpasolve(f==0, x);
true_roots =double(roots(:));
xl = 200;
xu = 300;
xr = (xl + xu) / 2;
es = 0.001;
xr_new(1) = xr;
if double(f(xl)) * double(f(xu)) >0
    disp('The function changes sign within this bound')
    for i = 1:100
        val(i) = double(f(xl)) * double(f(xr_new(i)));
        if val(i) < 0
            disp('The root lies in the lower interval')
            xu = xr_new(i);
        elseif val(i) > 0
            disp('The root lies in the upper interval')
            xl = xr_new(i);
        else val == 0;
            fprintf('The approximate root of the function is %1.2f \n',xr_new(i))
            break
        end
        xr_new(i+1) = (xl + xu) / 2;
        ea = abs((xr_new(i+1) - xr_new(i))./xr_new(i+1));
        if ea < es
            break
        end
    end
else
    disp('The function does not change sign within this bound')
end
    The function changes sign within this bound
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
The root lies in the upper interval
    % Print the results
ea = ea*100;
fprintf('The absolute approximate error is: %1.5f \n',ea)
    The absolute approximate error is: 0.06515 
    n_iterations = i+1;
fprintf('The total number of iterations are: %d \n',n_iterations)
    The total number of iterations are: 9 
    root = xr_new(1,end);
fprintf('The approximate root of the function is: %1.5f \n', root)
    The approximate root of the function is: 299.80469 
    x1 = -1000 : 1000;
y1 = double(f(x1));
xmin = -1000; xmax = 1000; ymin = -0.5; ymax = 0.5;
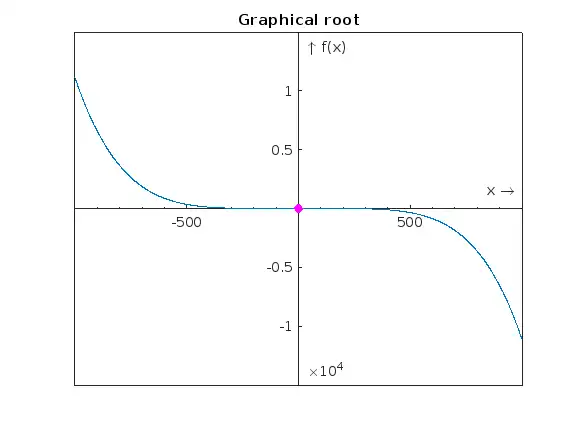
figure(1)
plot(x1, y1)
hold on
plot(true_roots,0,'mo','MarkerFaceColor','m')
set(gca,'XAxisLocation','origin','YAxisLocation','origin','XMinorTick','on')
xlabel('x \rightarrow')
ylabel('\uparrow f(x)')
title('Graphical root')
hold off

     

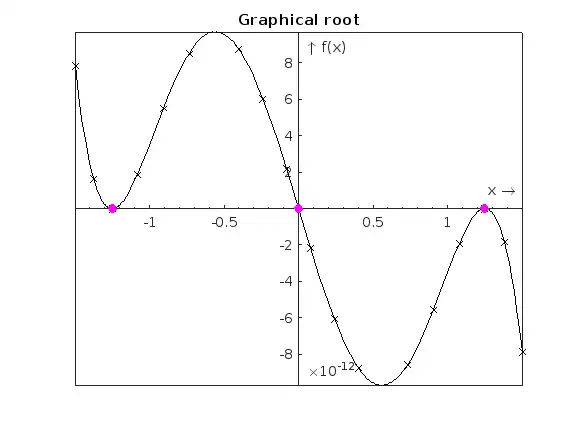
    figure(2)
Fun = @(x) (w0/(120*E*I*L))*(-x.^5+2*(L^2)*(x.^3)-(L^4)*x);
fplot(Fun, [-1.5, 1.5], 'kx-')
hold on
plot(true_roots,0,'mo','MarkerFaceColor','m')
set(gca,'XAxisLocation','origin','YAxisLocation','origin','XMinorTick','on')
xlabel('x \rightarrow')
ylabel('\uparrow f(x)')
title('Graphical root')

     


    Not satisfied with the answer ?? ASK NOW

    Get a Free Consultation or a Sample Assignment Review!

    Upload Assignment Talk to Expert