How to add two different surface curves in a single plot?
I have a bell shaped curve in 3D (generated from curve fitter app) as shown in the figures. Both are the same curve the only difference is one is without point data and the other has point data. Problem: I want to add another surface to the same plot for the same data which is at z=1 and parallel to x- and y-axis. Also, is it possible to find the values of major and minor axes of the ellipse formed from the intersection of both the surfaces. Or in other words, the values between the intersection of x and z values of both the curves and the y and z values of both the curves. I hope I am able to express myself clearly.
Prashant Kumar answered .
2025-11-20
[X,Y] = ndgrid(-3:0.1:3); f = @(x,y) exp(-(x.^2+(2*y).^2)*0.5); Z = f(X,Y)*3; figure surf(X, Y, Z) hold on surf(X, Y, ones(size(Z)), 'FaceColor','r', 'FaceAlpha',0.5, 'EdgeColor','none') hold off colormap(turbo)
figure
[c,h] = contour(X, Y, Z, [1 1]);
axis('equal')
grid
Ax = gca;
Ax.XAxisLocation = 'origin';
Ax.YAxisLocation = 'origin';
elpsfcn = @(b,xy) xy(1,:).^2/b(1)^2 + xy(2,:).^2/b(2)^2 - b(3);
opts = optimoptions('fminunc', 'MaxFunctionEvaluations', 5E+3, 'MaxIterations',1E+4);
[B, fv] = fminunc(@(b) norm(elpsfcn(b,c(:,2:end))), rand(3,1), opts)
Local minimum possible.
fminunc stopped because it cannot decrease the objective function
along the current search direction.
B = 3×1
52.8204
26.4510
0.0008
fv = 1.2653e-05
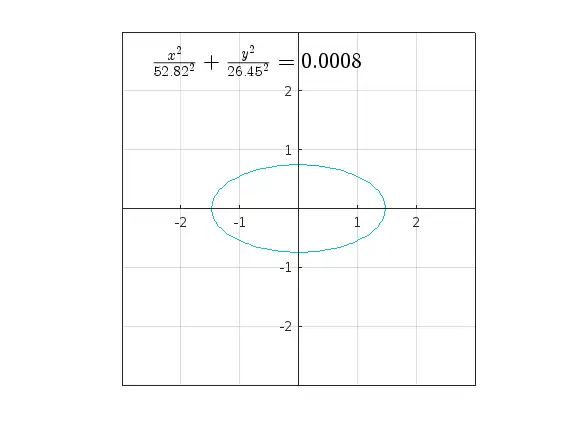
fprintf('Semimajor Axis = %.4f\nSemiminor Axis = %.4f\nConstant = %.4f\n', B)
Semimajor Axis = 52.8204 Semiminor Axis = 26.4510 Constant = 0.0008
text(-2.5, 2.5, sprintf('$\\frac{x^2}{%.2f^2} + \\frac{y^2}{%.2f^2} = %.4f$',B), 'Interpreter','latex', 'FontSize',16)
