natural cubic spline interpolation of y-values: how to get derivative of the spline wrt the y-values?

SA-W - 2023-03-16T10:32:10+00:00

Question: natural cubic spline interpolation of y-values: how to get derivative of the spline wrt the y-values?

Given a data set with support points x_1,...,x_n and corresponding y-values y_1,...,y_n.   My objective is to create a cubic spline f (with natural boundary conditions) that passes through the y_values. There are, of course, plenty of functions for doing this.   However, for a parameter identification procedure, I have to compute the derivative of the spline f with respect to the y-values -- at arbitrary points within [x1, x_n].   Is there an easy way using built-in functions of Matlab to compute the sensitivities?

Related Questions

Expert Answer

Prashant Kumar answered . 2025-11-20

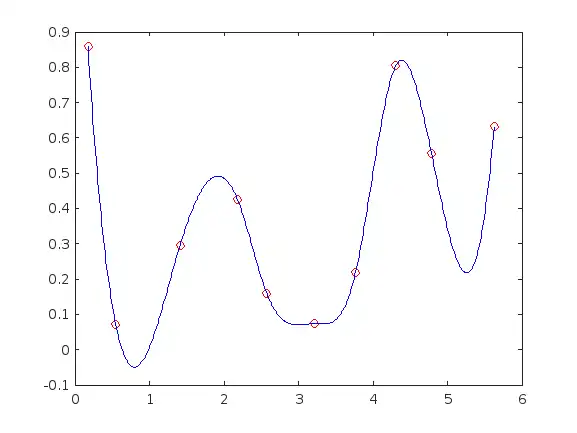
x=cumsum(rand(1,10));
y=rand(size(x));
xi=linspace(min(x),max(x),500);
f=ppval(spline(x,y),xi)

f = 1×500
    0.8578    0.8215    0.7861    0.7516    0.7180    0.6852    0.6533    0.6223    0.5920    0.5627    0.5341    0.5063    0.4794    0.4532    0.4278    0.4032    0.3794    0.3563    0.3340    0.3124    0.2915    0.2714    0.2519    0.2332    0.2152    0.1978    0.1812    0.1652    0.1498    0.1351

plot(x,y,'or',xi,f,'b') % 

b=eye(length(x));
yd=spline(x,b);
dfdy=ppval(yd,xi); % dfdy(i,j) is the derivative of f(xi(j)) with respect to y(i))
figure
plot(xi,dfdy')

Not satisfied with the answer ?? ASK NOW