random vector v from uniform distribution at (0,1) with sum(v)=1

Illustration
jimaras - 2022-06-17T12:20:50+00:00
Question: random vector v from uniform distribution at (0,1) with sum(v)=1

Hello, How can I generate a uniformly distributed random vector with its sum to be equal to 1?

Related Questions

  • random vector v from uniform distribution at (0,1) with sum(v)=1

    • Expert Answer

    Profile picture of Prashant Kumar Prashant Kumar answered . 2025-11-20

    Too many people think that generating a uniform sample, then normalizing by the sum will generate a uniform sample. In fact, this is NOT at all true.
     
    A good way to visualize this is to generate that sample for the 2-d case. For example, suppose we do it the wrong way first?
     
    xy = rand(100,2);
plot(xy(:,1),xy(:,2),'.')

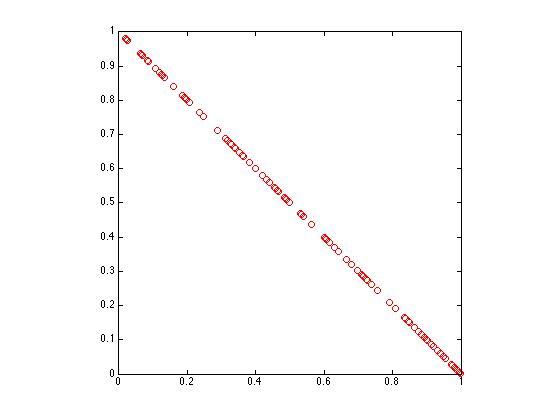
    Now, lets do the sum projection that virtually everyone poses. (Yes, it is the obvious choice. Now we will see why it is the wrong approach.)

     

    xys = bsxfun(@rdivide,xy,sum(xy,2));
hold on
plot(xys(:,1),xys(:,2),'ro')
axis equal
axis square

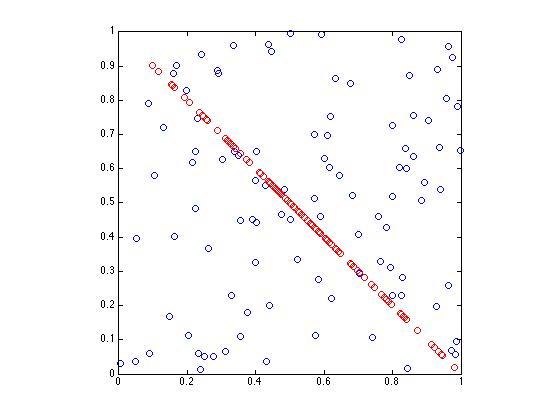
    distribution

    The sum-projected points lie along the diagonal line. Note the distribution seems to be biased towards the middle of the line. A uniform sample would have points uniformly distributed along that line.
     
    In a low number of dimensions there are some nice tricks to generate a sample that is indeed uniform. I tend to use Roger Stafford's submission to the file exchange, randfixedsum. It is efficient, and works in any number of dimensions.
     
     
    figure
xyr = randfixedsum(2,100,1,0,1)';
plot(xyr(:,1),xyr(:,2),'ro')
axis equal
axis square

    distribution


    Not satisfied with the answer ?? ASK NOW

    Get a Free Consultation or a Sample Assignment Review!

    Upload Assignment Talk to Expert