Generate synthetic data (or probability distribution object) from user-defined distribution function
need to generate a synthetic dataset using a distribution that is not supported by the Matlab stats toolbox. The distribution is a Type II Pareto (or Lomax) with the probability density function f ( x ) = ( a m^a) / ( m + x )^( 1 + a ), where a is a shape parameter and m is the minimum permissible value of x. The distribution also needs to be truncated at x=50. Is it possible to generate a probability distribution object (pd) from an equation or PDF, so that I can then use the "random" function to create the synthetic dataset? Or any other way to do this? Right now, I'm using "randsample" to do this, but that imposes a finite range or truncation on the PDF since it's an array.
John Michell answered .
2025-11-20
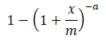
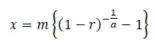
% Lomax PDF parameters:
m = 1;
a = 2;
% Draw random samples from uniform distribution in range 0 to 1:
n_samples = 100000;
r = rand(n_samples,1);
% Find the CDF values corresponding to the samples
x = m*((1 - r).^(-1/a)-1); % Inverse Lomax CDF
% Calculate histogram with bin width 0.1:
binwidth = 0.1;
bins = 0:0.1:5;
N = histcounts(x,bins); % Number of x values in each bin
f = N/n_samples/binwidth; % Observed frequency per x unit
bin_centres = (bins(1:end-1)+bins(2:end))/2;''
figure;
bar(bin_centres,f)
% Compare with analytic pdf
x = 0.05:0.1:4.95;
p = a/m*(1+x/m).^-(a+1); %Lomax PDF
hold on;
h = plot(x,p,'ok'); % Plot the PDF using circles
set(h,'MarkerFaceColor','w')
hold off
str = sprintf('Lomax PDF, m = %3.1f, a = %3.1f',m,a);
title(str)
legend('Sampled','Analytical')